Decrement Factor for grounding design 101 easy explanation

Decrement Factor for grounding design

Decrement factor D_f is basically the ratio between the rms value of the asymmetrical fault current to the symmetrical grounding fault current. I_G is the maximum asymmetrical alternating current flowing from the grounding grid to the surrounding earth, which includes the rms symmetric alternating current, Ig and the decaying DC component i_dc. The DC offset in the fault current is the difference between the ideal symmetrical currnet waveform and the actual current waveform. Mathematically, the actual current waveform can be divided into two parts, a symmetrical alternating current component and a unidirectional (DC) component.

$i(t) = I_m \sin(\omega t + \phi) + I_{dc} \cdot e^{-t / \tau}$

Where I_m is the peak of symmetric current, ω is the angular frequency in rad/s, ϕ is the phase angle at fault, I_dc is the initial dc offset and 𝜏 = L/R which is the time constant, ratio of inductance to resistance.

The DC component never oscillates, it starts with certain polarity either positive or negative and maintains that polarity over time as it decays. The DC offset decays exponentially over time. The polarity depends on fault initiation point, if the fault occurs at current zero, the dc offset will be maximum and vice versa.

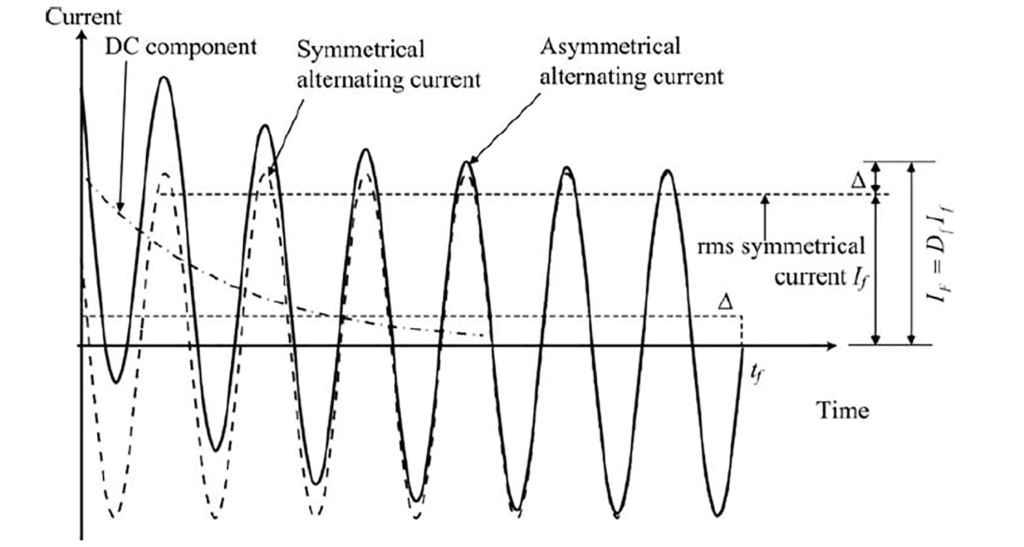
During the design of the grounding, the non symmetrical current component has to be taken into account. Because the dc offset present in the initial cycles of the fault current, causes the waveform to be asymmetrical. If it is not accounted in the design, it will lead to over stressing of grounding components.

The decrement factor D_f which is the ratio of the rms value of the asymmetrical fault current I_F to the rms value of symmetrical fault current I_f along with the DC offset ∆, where

$[\Delta = \frac{1}{t_f} \int_0^{t_f} i_{\text{dc}}(t) \, dt]$

The asymmetrical fault current consists of multiple components of current like transient, sub-transient and steady-state AC components along with unidirectional DC offset current component. The sub-transient component decays very quickly after the fault and transient AC components decays slowly than the sub transient component while the steady state component settles after the transient dies out, the DC offset current component decays exponentially with time.

According to IEEE Standard 80-2000, for a conservative and easy design, AC components are considered to be constant over time while only the DC component decays. Therefore, the asymmetrical fault current, can be expressed as

$i_f(t) = \sqrt{2} \, U_Y \left[ \sin \left( \omega_t + \alpha - \theta \right) - \exp \left( -\frac{t}{T_a} \right) \sin \left( \alpha - \theta \right) \right]$

where U is the pre-fault rms line to neutral voltage (in V), ω is the frequency (in radians/s), α is the voltage angle at the initiation of fault (in radians), θ is impedance angle of the system (in radians), Y is the equivalent AC system admittance (in mhos) and T_a is the time constant of the DC offset component in s; T_a = X/ ωR , where the X and R of the system sub-transient fault impedance in the location of the fault for a given type of fault are used to determine the ratio X/R.

However, for efficient grounding design, it is essential to consider faults with worst case of DC offset, that is maximum possible DC offset to be present in the asymmetrical current. When α – θ = – π/2 , putting it in the above Equation, the DC offset component is at the maximum, then Equation changes to

$i_f(t) = \sqrt{2} \, U_Y \left[ -\cos \left( \omega_t \right) - \exp \left( -\frac{t}{T_a} \right) \right]$

While optimizing the design for human safety, to avoid ventricular fibrillation and as its data is based on symmetrical current, we have to translate the equation to equivalent rms value for proper risk evaluation and thus mitigation. Therefore, by integrating the above equation squared over the entire duration of fault t_f

$I_F = \sqrt{\frac{1}{t_f} \int_0^{t_f} i_f^2(t) \, dt}$

where I_F is the effective rms value of the non-symmetry current in the whole fault duration and t_f is the duration of fault (in s).

Therefore, from the above two equations:

$I_F = I_f \sqrt{\frac{2}{t_f} \int_0^{t_f} \left[ \exp \left( -\frac{t}{T_a} \right) - \cos (\omega t) \right]^2 \, dt}$

MATHEMATICAL EXPRESSION FOR DECREMENT FACTOR

The decrement factor D_f is the mathematical ratio of I_F and I_f

D_f= I_F / I_f

$D_f = \sqrt{1 + \frac{T_a}{t_f} \left[ 1 - \exp \left( -\frac{2 t_f}{T_a} \right) \right]}$

Based on this equation, the decrement factor corresponding to different X/R ratio and fault durations can be calculated. We know that X/R is directly proportional to the time constant L/R, which can characterize how quick the dc offset decays. A large X/R ratio means a large time constant and dc offset decays slowly with small attenuation velocity. Apparently, the integral of the squared fault current, as above is determined by the attenuation velocity of the subtransient, transient AC component and DC offset. The solution becomes complex as the asymmetrical fault current is not a pure sine wave, each component decays at different rates, and more.

Usually values of the decrement factor which corresponds to different X/R and fault durations is used from the standards. An example in Tabulature form is shown below, with frequency of 50Hz. If the fault duration lies between two data, with linear interpolation we can obtain the required value.

Table for decrement factor selection

Fault Duration t_𝑓 (s)	Decrement factor D_f
Fault Duration t_𝑓 (s)	X/R = 10	X/R = 20	X/R = 30	X/R = 40
0.01	1.576	1.648	1.675	1.688
0.02	1.462	1.576	1.623	1.648
0.05	1.269	1.417	1.497	1.544
0.1	1.148	1.269	1.355	1.417
0.2	1.077	1.148	1.213	1.269
0.3	1.052	1.101	1.148	1.192
0.4	1.039	1.077	1.113	1.148
0.5	1.031	1.062	1.091	1.120
0.75	1.021	1.042	1.062	1.082
1.0	1.016	1.031	1.047	1.062

When the duration exceeds 30 cycles that is 600ms at 50 Hz frequency, the dc component of the fault current decays completely with negligible asymmetry left in the waveform then the decrement factor conforms to unity.

During auto reclosing several closely spaced fault currents are directed to the grounding grid. This leads to repeated high current surges to the ground which produces a cumulative stress on the grounding grid. Earlier practice used the shortest shock duration for determination of the decrement factor while taking the total time duration as sum of all durations for application of the decrement factor. This resulted in non conservative design estimate specially to worst cases of multi shock fault currents as in case of auto reclosing.

The transient AC and DC components depends on the X/R ratio, which is circuit’s reactance to resistance. But it doesnot includes the actual path resistance of the fault current which is present in grounding grids and tower footings. It therefore leads to a error between the calculated D_f and the actual D_f. The value of actual D_f will be lower because of the fault path resistance which is unaccounted and this overestimation of the D_f results in safer design calculation. However, for precise calculation, thorough network analysis has to be done.

This article is a part of the Safety and Earthing page, where other articles related to topic are discussed in details.

Decrement Factor for grounding design 101 easy explanation