
The Carnot cycle is the thermodynamic power cycle that was introduced by a French military Engineer, Nicolas Léonard Sadi Carnot in the year 1824 in his work, “reflection on motive power of fire”. It is a theoretical power cycle which is reversible with conserved entropy.
Table of Contents
Working
The Carnot cycle is an ideal cycle that is applied between a heat source and a heat sink, which releases work done on the transfer of energy from a hot source to a cooler sink. Consider a piston-cylinder arrangement, which is thermally insulated, the working fluid inside the cylinder takes the heat from the source during expansion and rejects the heat to the sink during the compression.
Or, reversibly, work can be put into the system for transferring energy from a cool sink to a hot source, making it a heat pump or refrigerator.
Thermodynamic Processes involved
The Carnot cycle comprises an isothermal expansion followed by an isentropic expansion, an isothermal compression along an isentropic compression.
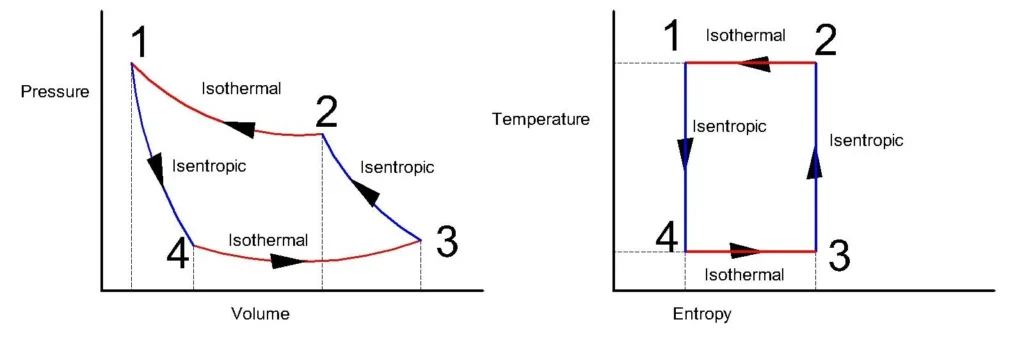
P-V and T-S Diagram of Carnot cycle.

During the process 1-2, heat is added by the source to the working fluid and it expands isothermally at a temperature T1. Heat addition during the isothermal process, Q1=2.3mRT1log (r), where r = V2/V1 is the expansion ratio.
During process 2-3, which is an isentropic process, the flow of heat is zero, and the expansion of fluid is at constant entropy as the temperature drops from T1 to T3.
During the process 3-4, the working fluid is compressed, while losing the heat to the sink at a constant temperature T3. Heat rejection during the isothermal process, Q2 = 2.3mR T3 log (r), where r = V3/V4 is the compression ratio and is equal to the expansion ratio.
During process 4-1, the fluid is compressed isentropically with no exchange of heat from the system with a temperature rise from T3 to T1.
Therefore, work done in the cycle is equal to the heat supplied – heat rejected = Q1– Q2
And thermal efficiency of the Carnot cycle is the ratio output which is workdone to the input which is heat addition at the source.
η = (Q1 – Q2) / Q1 = 1 – Q2 / Q1 = 1 – [2.3mR T3 log (r) / 2.3mR T1 log (r)]
η = 1 – T3 / T1.
Since this power cycle is completely reversible, it therefore can operate as a heat pump as the heat Q2 is added during the isothermal expansion at cooler temperature T2 during the process 4-3 while during the isothermal process 2-1, heat is rejected at a hotter temperature T1. The work W will be required this time on the heat pump contrary to the work produced while the cycle is used as a heat engine between the two thermal reservoirs.
Limitations of the Carnot cycle:
- It is impossible to achieve a frictionless thermodynamic process and thus reversibility of the cycle is lost in friction.
- It is not possible to transfer heat from a thermal reservoir without any temperature difference between the source or sink and the working fluid.
- The constant entropy is impossible to achieve in real-life applications as it requires very fast movement of the piston so heat transfer during the process can be neglected because of the almost zero time availability of the isentropic process. However, to achieve a constant temperature thermodynamic process, the speed of the piston is required to be very slow so that temperature difference does not come into the picture during heat transfer.
- Since both processes isothermal and isentropic happen to be in the single stroke of the piston, therefore a very slow movement accompanied by very fast movement is impossible to achieve in real-life applications.
Conclusion:
The Carnot cycle provides a benchmark for heat engines’ performances because of its ideal reversible thermodynamic processes, it achieves the highest efficiency of any heat engine that can ever be achieved in real engineering applications. All practical heat engines thus are compared to the Carnot’s efficiency for the purpose of finding gaps by evaluating and improving on it.
