Parallel plate capacitor: 101 Ideal Basic

Capacitance of Parallel-Plate Capacitor

The capacitance of a capacitor can be calculated from its electrical properties using the relation C = Q/V. However, at times it is desirable to calculate the capacitance of a capacitor in terms of the dimensions and relative permittivity of the dielectric or insulating medium. Although there are many forms of capacitors, the most important arrangement is the parallel plate capacitor.

Capacitance of Parallel-Plate Capacitor with Uniform Medium

Let us take a parallel plate capacitor that has two plates, each with an area of A square metres which are separated from each other by a uniform dielectric medium of thickness d metres with relative permittivity of ε_r as shown below. Let a potential difference of V volts be applied between the plates and place a charge of +Q and − Q on the plates. With reasonable accuracy, it can be assumed that the electric field between the plates is uniform.

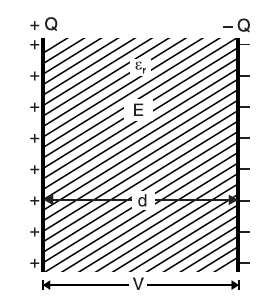
Electric flux density between plates is

D = Q/A coulomb/m2

The electric intensity between plates is

E = V/d

But D = ε₀ ε_r E

or Q/A = ε₀ ε_r V/d

or Q/V = (ε₀ ε_r A) / d

The ratio of charge to voltage or Q/V is the capacitance C of the capacitor.

C = (ε₀ ε_r A) / d …. For a medium

C = (ε₀ A) / d …. For air

IMPORTANT POINTS:

Capacitance is directly proportional to relative permittivity ε_r and area of the plates A and inversely proportional to the dielectric thickness d.

The relative permittivity of the medium is the ratio between the capacitance of the medium to the capacitance of air.

C_medium / C_air = ε_r.

Re-arranging the relation for C in air

ε₀ = C d / A = farad * meter / meter² = farad/meter.

Therefore, permittivity can also be measured in F/m.

Parallel Plate Capacitor with Composite Medium

In these parallel plate capacitors, let the space between the plates be occupied by three dielectrics of thicknesses d₁, d₂ and d₃ metres and relative permittivities ε_r1, ε_r2 and ε_r3 respectively as shown in Figure. The electric flux density D in the dielectrics remains the same and is equal to Q/A, as the total charge on each plate is Q, hence Q coulombs is also the total electric flux through each dielectric.. However, the electric intensities of this parallel plate capacitor will be different in the three dielectrics and are given by;

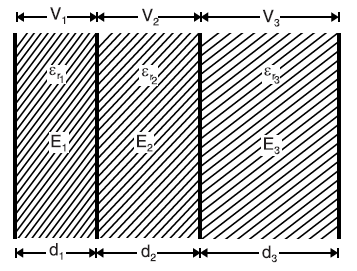
E₁ = D / ε₀ ε_r1 ; E₂ = D / ε₀ ε_r2 ; E₃ = D / ε₀ ε_r3

If V is the total potential difference across the capacitor and V1, V2 and V3 the potential difference across the three dielectrics of the parallel plate capacitor respectively, then,

V = V₁ + V₂ + V₃

= E₁d₁ + E₂d₂ + E₃d₃

= (D / ε₀ ε_r1) * d₁ + (D / ε₀ ε_r2) * d₂ + (D / ε₀ ε_r3) * d₃

= D/ ε₀ [ d₁ / ε_r1 + d₂ / ε_r2 + d₃ / ε_r3]

= Q / (A ε₀)[ d₁ / ε_r1 + d₂ / ε_r2 + d₃ / ε_r3]; since D = Q/A

Or Q/V = A ε₀ /  [ d₁ / ε_r1 + d₂ / ε_r2 + d₃ / ε_r3].

Since Q/V is the capacitance, therefore,

C = A ε₀ /  [ d₁ / ε_r1 + d₂ / ε_r2 + d₃ / ε_r3] farad

Different cases

We shall discuss the following two cases :

Medium partly air in a parallel plate capacitor

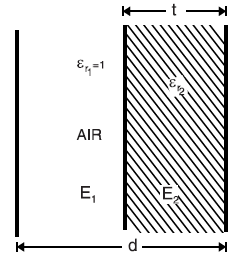
As shown in the figure a parallel plate capacitor has plates d metres apart. Suppose the medium between the plates consists partly of air and partly of dielectric of thickness t metres and relative permittivity εr2. Then the thickness of air is d − t. Using the relation above, we shall have

C = A ε₀ / [(d-t)/1 + t/ ε_r2]; since relative permittivity of air is 1

= A ε₀ / [d-(t-t/ ε_r2)] farad

When the dielectric slab was introduced in parallel plate capacitor

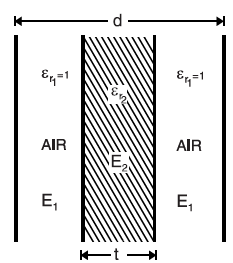
As shown in the figure a parallel-plate air capacitor has plates d metres apart. Suppose a dielectric slab of thickness t metres and relative permittivity ε_r2 is introduced between the plates of the capacitor. Using the relation above, we shall have

C = A ε₀ / [(d-t)/1 + t/ ε_r2]; since relative permittivity of air is 1

= A ε₀ / [d-(t-t/ ε_r2)] farad

Special Cases of Parallel Plate Capacitor

We have seen that the capacitance of a capacitor depends upon plate area, thickness of dielectric and value of relative permittivity of the dielectric. We consider two cases by way of illustration.

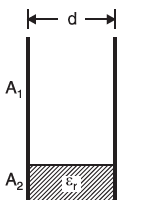
In the figure, it is shown that dielectric thickness is d but the plate area is divided into two parts; area A1 has air as the dielectric and area A2 has dielectric of relative permittivity εr. The arrangement is equivalent to two parallel capacitors. Their capacitances are :

C₁ = A₁ ε₀ / d, C₂ = A₂ ε₀ ε_r / d

Therefore, total capacitance for this parallel plate capacitor is:

C = C₁ + C₂

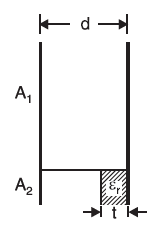
In the figure, it is shown that the plate area is divided into two parts, area A₁ which has a dielectric (air) of thickness d and area A₂ having a dielectric (ε_r) of thickness t and air occupies the remaining thickness.

This is equivalent to two capacitors connected in a parallel arrangement. Their capacitances are:

C₁ = A₁ ε₀ / d , C₂ = A₂ ε₀ / [d-(t-t/ ε_r)]

Hence, equivalent capacitance for this parallel plate capacitor is:

C = C₁ + C₂

Factors affecting the capacitance of parallel plates

The factors influencing the capacitance are listed below:

Area of the plates: It is evident from the formula that the capacitance is directly proportional to the area of the plates. The bigger the area the more will be capacitance as more charges will be attached to the enhanced surface area.

Size of dielectric: From the above formula for the capacitance, it is evident that the thickness of the dielectric d is inversely proportional to the capacitance. Hence, the increased size of the dielectric will decrease the capacitance.

Selection of dielectric material: The relative permittivity of the insulating medium ɛ_r is directly proportional to the capacitance. Hence, the capacitance is influenced by the selection of dielectric material.

Applications of Parallel plate capacitor

• Extensively used in RC timing circuits.
• Used in filtering circuits to filter out the noise.
• Used in amplifiers to block DC signals while coupling AC signals.
• Used in the flash for photography.