Energy Stored in a Capacitor
Charging of a capacitor means transferring electrons between the plates of the capacitor through the dielectric medium. This process of electron transfer is possible only at the expense of energy because the electrons have to be moved against the opposing forces in the dielectric medium. The energy expended in moving the electrons gets stored in the electrostatic field set up in the dielectric medium. During the discharging of the capacitor, the field collapses and the stored energy is released at once.
Table of Contents
Considering a capacitor of C farad, charged from a DC source of V volts. At any random stage of charging, let the charge on the capacitor be q coulomb and the potential difference across the plates is v volts.
Then, capacitance, C = q/v
At this instant, v joules of work is needed for transferring 1 C of charge from one plate to the other. If further small charge dq is transferred, then the work done is
dW = v dq = C v dv, [since C = q/v, q = C v, therefore, dq = C dv]
The total work done in raising the potential of the uncharged capacitor to V volts is
W = 0∫V C v dv = C [V2/2]V0
W = ½ C V2 joules
This work done gets stored in the electrostatic field set up in the dielectric medium of the capacitor.
Energy stored in a capacitor is, E = ½ C V2 = ½ Q/V * V2 = ½ QV [since C=Q/V]
Or, E = Q2 / 2C [since V=C/Q]
It may be noted that an ideal capacitor does not release or consume energy, instead, it only stores the energy in the electric field.
Energy Density of Electric Field
The energy stored in a Capacitor per unit volume of the electric field is called the energy density of the electric field
Energy density, u = Total energy stored in a capacitor (U) / Volume of the electric field.
It is seen that the expended energy gets stored in the electric field of the capacitor. In fact, wherever an electric field exists, there is stored energy. When the electric fields are in consideration, the energy density (u) i.e. energy stored in a Capacitor per unit volume is of most concern.
In the case of a charged parallel plate capacitor the area of the plates and the separation between the plates are as shown in the figure below
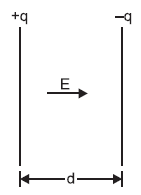
Energy stored in the electric field of the capacitor is, E = ½ C V2
The volume of space between plates = Ad
Therefore, Energy density in the electric field of the capacitor, u = Energy stored in the Capacitor / Volume = CV2/2Ad
Since the capacitance of the parallel plate capacitor is C = ε0A/d.
Therefore, u = ε0A/d * V2/2Ad = ½ ε0 (V/d)2
But, the ratio of V/d is the intensity of the electric field (E) existing between the plates of the capacitor.
Therefore, Energy density, u = ½ ε0 E2…….for air
u = ½ ε0 εr E2……….for other medium
The unit of energy density will be joules/m3.
Therefore, energy density (i.e., electric field energy stored in a Capacitor per unit volume) in any region of space is directly proportional to the square of the electric field intensity in that region. The density of energy in the electric field of the capacitor can also be expressed in terms of the electric flux density D (= CE).
U = ½ DE = D2/2 ε0 εr
Force on Charged Plates
Let us consider two parallel conducting plates x meters apart and carrying constant charges of +Q and −Q coulombs respectively. And the force of attraction between the two plates of the capacitor is F newtons. If one of the plates is moved away from the other by a small distance dx, then the work done is
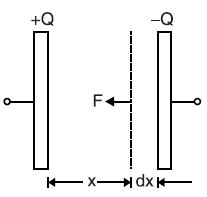
Work done = F × dx joules
Since the charges Q on both of the plates remain almost constant, no electrical energy can either enter or leave the system during the movement dx.
Work done = Change in energy stored in a capacitor
Initial stored energy = ½ Q2/C joules
Since the separation of the plates of the capacitor has increased from X to X + dx, the capacitance of the capacitor will decrease by dC. The final capacitance of the capacitor is, therefore, (C − dC).
Final stored energy = ½ Q2/C-dC
Multiplying the numerator and denominator by (C+dC) we get,
= ½ Q2(C+dC) / [C2-(dC)2]
Since dc is smaller than C then (dC)2 can be neglected compared to C2
Therefore, the final stored energy is = ½ Q2(C+dC) / C2 =Q2/2C + Q2/2C2 dC
Change in stored energy is = Q2/2C + Q2/2C2 dC – Q2/2C = Q2/2C2 dC
Now equating, F × dx = Q2/2C2 dC or, F = Q2/2C2 dC/ dx
F = ½ V2 dc / dx [since C=Q/V]
Now, C = ε0 εr A /x
Therefore dC/dx = – ε0 εr A/x2
Therefore, F = ½ V2 dC/ dx = – ½ V2 (ε0 εr A/x2) = – ½ ε0 εr A (V/x)2
As V/x is the electric intensity,
F= – ½ ε0 εr AE2……for medium
F= – ½ ε0 AE2……for air
The above equation represents the force between the plates of a parallel-plate capacitor charged to a potential difference of V volts. The negative sign in the equation represents attraction.
Note: The force of attraction between charged plates may be utilized as a means of measuring the potential difference. An instrument of such kind is known as an electrostatic voltmeter.

