Electrical Resistance may be defined as the property of a substance due to which it opposes or restricts the flow of electricity or its transmission i.e., electrons passing through it. Metallic classes, acids, and solutions of salt can conduct electricity efficiently. However, among the pure metals, silver, copper, and aluminum are considered very good conductors because of their atomic structure, given in order. This happens because of the presence of a large number of loosely attached electrons in their atoms. The loose electrons always assume a motion that is definite and directed only on the application of an electric potential which causes the potential difference forcing the motion.
Table of Contents
The electrons whilst set in motion, pass through the molecules or the atoms of the conductor material, attaining collision with other atoms and electrons, producing heat or losing energy. Those substances that offer relatively greater difficulty or hindrance to the passage of these electrons are said to be relatively poor conductors of electricity like Bakelite, mica, glass, rubber, p.v.c. (polyvinyl chloride) and dry wood etc. However, good insulators can include substances with fibers mostly found in dried paper and cotton, mineral oils that do not contain acids and water, ceramics such as porcelain and asbestos, and many other plastics. It is helpful to remember that electric friction resembles friction in Mechanics.
UNIT OF ELECTRICAL RESISTANCE
The SI unit of resistance is the ohm. Named after George Simon Ohm (1787-1854), a German mathematician who formulated the law in the year 1827, known after his name as Ohm’s Law.
A conductor has a resistance of one ohm when it allows one-ampere current to flow through it at one volt of potential difference impressed across the conductor’s terminals.
![]()
or V = IR, where V is the potential difference, I is the current, and R is the resistance.
Generally, insulators have a very high resistance, and for the electrical insulators, a much bigger unit of resistance is used that is, mega-ohm = 106 ohm (mega means million), or kilo-ohm = 103 ohm (kilo means thousand). However, for very small resistances mostly used in electronics, smaller units of resistance like milli-ohm = 10−3 ohm or micro-ohm = 10−6 ohm are commonly used. The symbol for ohm is Ω.
LAWS OF ELECTRICAL RESISTANCE
The resistance ‘R’ in a conductor depends on the following factors:
- The resistance varies directly with the conductor’s length, l.
- It varies inversely to the cross-sectional area of the conductor, ‘A’.
- The nature of the material has an impact on the conductor’s resistance.
- Temperature significantly impacts the lattice vibration of a metal, thereby increasing the electrical resistance of the conductor.
Neglecting the last factor, It can be implied that
![]()
or ![]()
Where ρ is a constant known as the specific resistance or resistivity of the material. It depends on the nature of the conductor’s material.
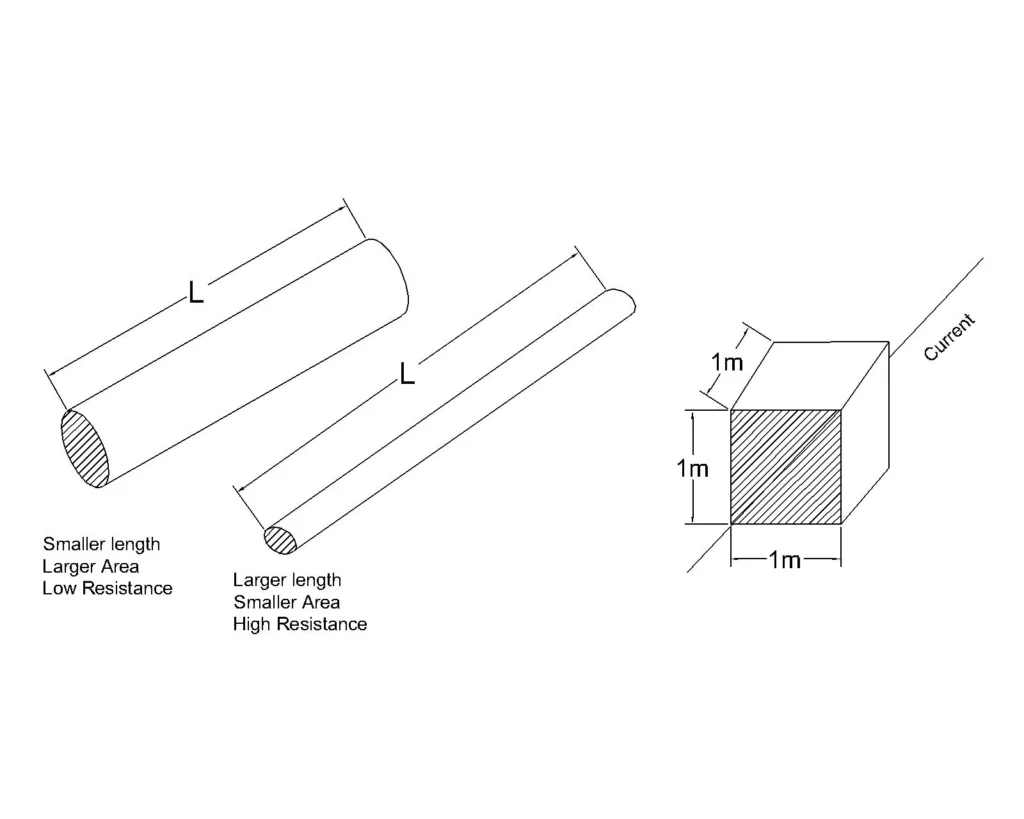
Upon considering the length of the conductor l to be 1m and the area of the conductor, A to be 1 m2, then the specific resistance of a material may be defined as the electrical resistance acting between the two sides of a cube of volume 1 m3 made of the same material.
The SI unit of resistivity, ρ is ohm-meter (Ω-m)
Resistivity of some materials
| Material | Resistivity at 20 degree C |
| Copper | 1.68 x 10-8 |
| Aluminium | 2.82 x 10-8 |
| Gold | 2.44 x 10-8 |
| Silver | 1.59 x 10-8 |
| Iron | 1 x 10-7 |
| Nickel | 6.99 x 10-8 |
| Lead | 2.20 x 10-7 |
| Tungsten | 5.6 x 10-8 |
| Graphite | 3 x 10-5 |
| Carbon black | 3.5 x 10-5 |
| Glass | 1010 – 1014 |
| Rubber | 1013 – 1016 |
| Dry Wood | 104 – 107 |
| Water | 2 x 105 |
| PVC | 1013 – 1015 |
CONDUCTOR VS INSULATOR
| Aspects | Conductor | Insulator |
| Resistance | Minimal | High |
| Electrical Conductivity | High | Minimal |
| Common Materials | Copper, aluminum, gold, silver | Rubber, glass, plastic, wood |
| Temperature Dependence | Conductivity decreases with temperature | Conductivity increases at high temperatures |
| Physical Characteristics | Metallic, shiny, ductile | Non-metallic, brittle or flexible |
| Applications | Electrical wiring, circuit components | Insulation for wires, protective coatings |
Effect of Temperature on ELECTRICAL Resistance
The effect of the rise in temperature on electrical resistance is as follows:
- to increase the resistance of pure metals. The increase in resistance is significant and fairly regular at normal temperature ranges. The temperature/resistance graph is a straight line and has a positive temperature coefficient of resistance.
- to increase the resistance of alloys, though in the case of alloys, the increase of resistance is small and it is much irregular. For some high-resistance alloys like Eureka (60% Cu and 40% Ni) and manganin, the increase in resistance is (or can be made) negligible over a considerable range of temperatures.
- to decrease the resistance of electrolytes, insulators, and partial conductors such as carbon. Hence, it is said that insulators have a negative temperature coefficient of resistance.
Effect of Geometric Factors on Electrical Resistance
As the length of a conductor increases, the resistance also increases because as the length becomes more, the collision of free electrons with the ions will increase. This can be thought of as stacking resistors in series. The more the number of resistors stacked, the more will be the equivalent resistance.
With the increase in the cross-sectional area of the conductor, the electrical resistance of the conductor decreases. This is because the resistance is inversely proportional to the cross-sectional area of a conductor. It can be thought of as piling up of resistors in parallel, the more number of resistors connected in parallel, the less will be the equivalent resistance. Another analogy can be the water pressure in a pipe with smaller diameter is more than a pipe with wider diameter.
Measurement of Electrical Resistance
The resistance can be measured with the help of an ohmmeter, multimeter, or a Wheatstone bridge.
Taking the multimeter settings to Ω as specified in the meter, we have to prepare the probes of the meter. One is connected to COM and the other to “V” marked in the meter for probe connection. After that, we connect the probe to the two ends of the resistor to be measured and take the reading of resistance from the display.
However, in the Wheatstone bridge, we can find the resistance of a resistor if the other three resistances are known to us.
Firstly, we have to take 2 known resistors and a variable resistor. By placing known resistor R1 and variable resistor R2 in one arm of the Wheatstone bridge, we have to place R3 and unknown resistor Rx in another arm. we have to connect a galvanometer across the arms for current reading.
Now by adjusting the variable resistor R2 such that the current across the arm is zero as on the galvanometer, we can find the unknown resistance Rx by the formula Rx = R3 * (R1/R2)

