CT CORE SIZING – KNEE POINT CALCULATION EASY EXPLAINED 102

The CT core sizing depends on the relay consideration for the feeder protection.

FOR METERING CT CORE SIZING:

The CT can be a multi-radio CT and the turns ratio or CTR can be calculated based on the estimated load/demand/requirement in the feeder. Also to take into consideration the future increment of load in the feeder, as a substation is optimally designed for 25 years.

The selection of the accuracy class of the metering core is based on the application as discussed in past articles.

The CT burden in VA is calculated based on the ammeter/ energy meter burden and interconnected lead cable burden.

Instrument Security Factor or ISF is essentially selected as low as possible. A value of ISF 5 is optimum for high-voltage applications.

FOR PROTECTION CT CORE SIZING P CLASS

The CTR has to be calculated based on load/demand.

The accuracy class may be selected based on requirements as per IEC or country standards such as 5P or 10P.

The CT secondary burden VA is to be calculated based on the secondary connected overcurrent or earth fault relay burden and interconnecting lead cable burden.

ALF is mostly selected as 10 or 20 depending on required accuracy.

FOR PROTECTION CORE PX CLASS

The CTR is to be selected based on load/demand.

CT knee point voltage has to be selected based on the relay used or relay requirements. I will discuss the knee point voltage calculation elaborately in the next articles.

Magnetizing current I_m commonly selected as 20,30 or 60mA.

Rct or resistance of the CT secondary winding required for calculation can be taken from the manufacturer or the concerned utility.

Let us consider a 220KV feeder to be protected with differential and distance protection and thereby put up a thorough CT core sizing calculation for the CT core.

The most fundamental step in the core sizing is the determination of CT knee point voltage and rest falls in place. The calculation of knee point voltage is discussed in detail.

Depending on the load of the feeder the chosen CTR is 2000/1000/1-1-1 A. Considering the main protections we shall design the PX core of the Current transformer.

The protection relays chosen for the purpose are ABB RED 670 and REL 670. From the application manual, we found the following formulae for calculating the Knee point voltage of the CT core.

CT CORE SIZING EQUATIONS FOR DISTANCE PROTECTION RELAY

E_al > E_{al req} = (I_kmax * I_sn) / I_pn  * a ( R_CT + R_L + S_R / I_r²)

E_al > E_{al req} = (I_kzone1 * I_sn) / I_pn  * k ( R_CT + R_L + S_R / I_r²)

CT CORE SIZING EQUATIONS FOR DIFFERENTIAL PROTECTION

E_al > E_{al req} = (I_{k max} * I_sn) / I_pn  * k ( R_CT + R_L + S_R / I_r²)

E_al > E_{al req} = (2 * I_{t max} * I_sn) / I_pn  * k ( R_CT + R_L + S_R / I_r²)

Where,

E_al =Equivalent limiting secondary emf

E_{al req} =Required rated equivalent limiting secondary emf

I_kmax = Maximum fault current for close-in faults.

I_tmax = Maximum fault current for through faults.

I_pn = Rated primary current of CT.

I_sn = Rated secondary current of CT.

I_r = Rated current of IED protection = Isn.

R_ct = Secondary resistance of CT.

R_l = Resistance of secondary lead.

SR = Burden of IED or Relay.

Therefore, CT _{knee point voltage} = Max E_al

DIFFERENTIAL RELAY EQUATIONS:

We know there are two types of faults based on the location of faults that are used in the CT core sizing

Close in Faults

Faults that are near to the substation and take the full amount of fault current in the calculation.

Any external / Remote end / Through Fault:

These faults reach the substation and occur at a distance from the substation. In this case, the transmission line impedance is also going to be added to the total impedance.

For the differential relay, the required voltage of the relay or CT knee point voltage can be derived from the calculation of the equations below for both types of faults.

E_al > E_{al req} = (I_{k max} * I_sn) / I_pn  * k ( R_CT + R_L + S_R / I_r²)

E_al > E_{al req} = (2 * I_{t max} * I_sn) / I_pn  * k ( R_CT + R_L + S_R / I_r²)

The value of I_Kmax can be derived from the tender specification.

However, the value of I_{t max} can be calculated in the following steps:

EXERCISE FOR THROUGH FAULT

Since the through fault depends on the line conductor’s resistance and reactance or total impedance value of the transmission line, we need to calculate the total reactance and resistance at the fault location.

Total resistance = Total source resistance (from generator till substation) + connected transmission line resistance.

Total reactance = Total source reactance (from generator till substation) + connected transmission line reactance.

Since the source of the fault current is the generator itself.

The source resistance and reactance or impedance can be found by equating the short circuit fault current.

In the event of a fault, the actual short circuit current consists of two components, the sinusoidal varying AC component and the exponential decaying DC component with a time constant that is based on system inductance  L and resistance R.

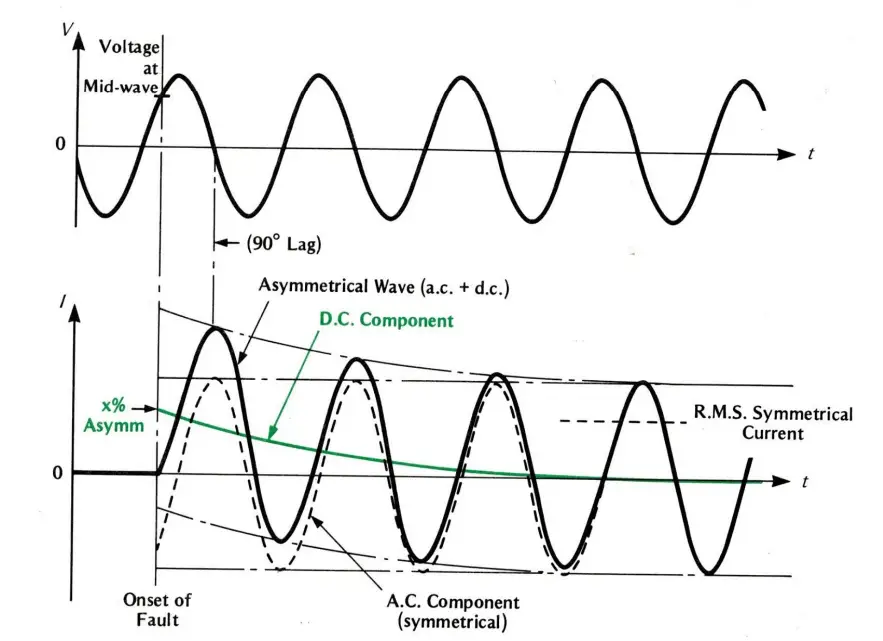
The bottom and the top envelop is the short circuit value at that instant.

The transmission line has inductance and capacitance which store energy and release it whenever there is a short circuit in the form of DC.

The DC component is nonperiodic and exponentially decays with time constant T_p

Where T_p = L/R, where L is the source inductance and R is the source Resistance.

With the help of L/R, we can also derive the source X/R ratio.

X/R = 2*3.14* f * L/R, where f is the frequency.

Also, T_p = t / (ln (√2 / %DC *100)), where t is the circuit breaker‘s breaking time and %DC is the CB’s DC current breaking capacity.

Design Criteria for ct core sizing:

Nominal system voltage: 220KV

Nominal System frequency: 50 Hz

Rated short circuit current: 63KA

CB DC current breaking capacity: 61% (from CB rating plate)

CB breaking time: 40ms

Therefore, T_p = 40 / (ln (√2 / 61 *100)) = 47.57 ms

X/R = 2*3.14* 50 * 47.57/1000 = 14.94 s

From the power impedance triangle, tan θ = X/R

θ = tan^-1 X/R = tan^-1 14.94 =86.18^θ

Therefore, cos θ = cos 86.18 = 0.067, sin θ= sin 86.18 = 0.997.

Now, source impedance Z_s = V_s / √3 * I_sc = 220*1000/1.732*63000 = 2.017 ohm.

Now, X_s = Z_s sin θ = 2.017 * 0.997 = 2.0109 ohm

R_s = Z_s cos θ = 2.017 * 0.067 = 0.1351 ohm

Now, from transmission line data:

Length = 3.7 KM, positive sequence impedance Z_l = 1.66 ohm, positive sequence Resistance R_Ll = 0.3552 ohm, positive sequence Recatance, X_Ll = 1.625 ohm, zero sequence Resistance, R_L0 = 0.89392 ohm, zero sequence Recatance X_L0 = 5.5278 ohm.

Zero sequence occurs in line with to ground fault and in the static system the positive and the negative sequence are equal.

Therefore, the positive sequence impedance of the line, Z_L1 = √(R_L1² + X_L1²) = √ (.355² + 1.625²) = 1.664 ohm.

Zero sequence impedance of the line, Z_L0 = √(R_L0² + X_L0²) = √ (0.893² + 5.527²) =5.572 ohm.

Since the zero sequence impedance is more than the positive sequence impedance of the line therefore it is clear that the maximum through-fault current will occur in L-L faults and not in L-G zero sequence faults. Therefore, we will not consider zero sequence impedance in the through-fault calculation for three phases.

Therefore, the total resistance R_th3 = R_s + R_L1 =0.135 + 0.356 =0.491 ohm.

Total reactance, X_th3 = X_s +X_L1 = 2.013 +1.625 = 3.638 ohm.

Impedance for through fault, Z_th3 = √(R_th3² + X_th3²) =√(0.491² + 3.638²) =3.671 ohm.

Therefore, the through fault current for three phases, I_tmax = V/1.732 Z_th3 = 220*1000/1.732*3.671 = 34602 A.

NB: It is to be noted that 1 time of line impedance is considered for conservative design.

Through fault current calculation for single phase fault:

Total impedance Z_T = positive sequence impedance Z₁ + negative sequence impedance Z₂ + zero sequence impedance Z₀.

The positive and negative sequence impedance of linear, symmetrical, and static circuits (cable feeder, transmission line, transformer & static loads) are equal and are the same as those used in the analysis of the balanced conditions. This is due to the fact that the impedance of such circuits is independent of the phase order, provided the applied voltages are balanced. Hence 2 times the positive sequence resistance & reactance are considered for the calculation of net resistance & reactance respectively for single phase fault.

Considering Z₁=Z₂

Therefore, Z_T = 2Z₁ + Z_0.

Resistance, R_th1 = 2(R_s+R_L1) + (R_s+R_L0) = 2(0.135+0.356) + (0.135+0.894) = 2.011 ohm

Reactance, X_th1 = 2(X_s+X_L1) + (X_s+X_L0) = 2(2.013+1.625) + (2.013+5.5) = 14.789 ohm

Impedance, Z_th1 = √(R_th1² + X_th1²) =√(2.011² + 14.789²) =14.925 ohm.

Through fault current for single phase I_th1 = 3*V/1.732 Z_th1 = 3* 220*1000/(1.732*14.925) = 25767A.

It is to be noted that I_fault = 3 * I_0, where I₀ is Zero sequence current.

Since it is now clear that the maximum through fault is in 3-phase faults, single-phase calculations can be avoided.

Therefore, the maximum through fault current, I_tmax = 34602 A

I_kmax = 63000A

R_CT = 10 ohm for 2000A primary and 5 ohm for 1000A primary,

R_L =  calculated from cable lead parameters.

R_relay = S_R/I_r² = 0.020/1 = 0.020 ohm, taken from the relay application manual.

Therefore, at tap 2000/,

E_al ≥ E_{al req} = (I_{k max} * I_sn) / I_pn  * k ( R_CT + R_L + S_R / I_r²)

E_al  ≥ 1.1(margin of 10%)* 63000 * ( 10 + 5.712 +0.02 ) * 1/2000 [considering a margin of 10% therefore multiplying with 1.1]

E_al  ≥546 V

Again, E_al ≥ E_{al req} = (2 * I_{t max} * I_sn) / I_pn  * k ( R_CT + R_L + S_R / I_r²)

E_al ≥ 1.1 * 2* 34602 ( 10 + 5.712 +0.02 ) * 1/2000 [considering a margin of 10% therefore multiplying with 1.1]

E_al ≥ 601 V

At tap 1000/1,

With a similar equation and changing the I_pn to 1000,

E_al ≥ 747 V for close in fault.

E_al ≥ 821 V for through fault.

Now according to the application manual, the E_knee is lower than E_al also it is as per IEC 60044-6

Therefore, E_knee = 0.8 * (max E_al) = 0.8 * 821 = 657 V.

FOR P CLASS CT CORE

We can derive the CT knee point voltage by

E_Knee ≥ E_alf = ALF * I_sec √ ((R_CT + R_b)² + X_b²), where R_b is the resistive part of the rated burden and X_b is the inductive part of the rated burden.

DISTANCE PROTECTION

The knee point voltage of CT can be found by solving the equation for distance protection as

E_{al ≥} E_{al req} = (I_kmax * I_sn) / I_pn  * a ( R_CT + R_L + S_R / I_r²)

E_al ≥ E_{al req} = (I_kzone1 * I_sn) / I_pn  * k ( R_CT + R_L + S_R / I_r²)

Here, a = a factor which is the function of the primary time constant of the decaying DC fault current. T_p, a = 2 for T_p ≤ 50ms and 3 for T_p >50 ms.

k = is a factor of the primary time constant for the DC component in the fault current for a three-phase fault at the relay set to zone-1 reach

K= 4 for T_p ≤ 25ms and 6 for T_p > 25ms

The time constant is the time required for the decay of the DC component of the fault current.

With the help of the DC component time constant, we can find the source X/R ratio as done in the previous part, X/R = 2*3.14 f T_p

And with the T_p, time constant value we can select the value of a and k to solve the distance relay equations.

It may be noted if T_p is more, the fault is away from the source and if it is less then it is close.

I_Kzone1 is the maximum primary fundamental frequency current for faults at the end of zone 1 reach. Also called as through fault contribution value. Since it depends on the line and source impedance, therefore, low impedance results in high short circuit current and vice versa.

 Therefore, for I_Kzone1 the total impedance  (resistance and reactance) needs to be found out. The total impedance is source impedance + line impedance.

Source resistance + line resistance= total resistance

Source reactance + line reactance = total reactance

Since the single-phase fault value is less than the 3-phase fault value, we can always ignore the single-phase fault in the calculation.

For close-in fault:

I_kmax= 63000KA

V= 220KV,

T_p = 47.57ms  [calculated as previous from values of CB name plate]

Therefore, a = 2

For 3-phase through faults

Source resistance = 0.135 ohm

Source reactance = 2.016 ohm

Line resistance = 0.356 ohm

Therefore 80% of line resistance = 0.8*0.356 = 0.284 ohm

Line reactance = 1.625 ohm

Therefore 80% of line reactance = 0.8*1.625 = 1.299 ohm

Total resistance = 0.135 + 0.284 = 0.413 ohm

Total reactance = 2.016 + 1.299 = 3.311 ohm

Total impedance Z_th3 = √(0.413² + 3.311²) = 3.340 ohm

Considering a 10% margin,

I_kzone1 = 1.1 V/√3 Z_th3 = 1.1*220*1000/(1.732*3.340) = 41840 A

X/R for 3phase through fault = 3.313/0.42 = 7.89

Therefore T_pth3 = (X/R)*1000/ 2*3.14 *f = 7.89 *1000 / 2 * 3.14 * 50 = 25.12 ms

Therefore, the value of k = 6

At tap 2000/1,

For close-in fault,

E_al ≥ 1.1*I_kmax*a*(I_sn/I_pn)*(R_ct+R_L+R_relay) = 1.1*63000*2*(1/2000)*(10+5.758+0.02) =1094V

For through fault,

E_al ≥1.1*I_kzone1*k*(I_sn/I_pn)*(R_ct+R_L+R_relay) = 1.1*41840*6*(1/2000)*(10+5.758+0.02) =2179 V

At tap 1000/1 A,

For close-in fault,

E_al ≥ 1.1*I_kmax*a*(I_sn/I_pn)*(R_ct+R_L+R_relay) = 1.1*63000*2*(1/1000)*(5+5.758+0.02)=1494V

For through fault,

E_al ≥1.1*I_kzone1*k*(I_sn/I_pn)*(R_ct+R_L+R_relay) = 1.1*41840*6*(1/1000)*(5+5.758+0.02) =2977 V

Therefore, E_knee = 0.8 * (max E_al) = 0.8 * 2977 = 2382 V.