Capacitance of an Isolated Conducting Sphere
The capacitance of sphere, an isolated spherical conductor can be calculated by assuming that the “missing” plate is Earth (zero potential). Let us consider an isolated sphere of metal with a radius r is placed in a medium of relative permittivity ɛr. Let charge +Q be given to this sphere-shaped conductor.
Table of Contents
The charge spreads over the surface uniformly. Therefore, in order to find the potential at any point on the surface of sphere (or outside the sphere), we can assume that the entire charge + Q is concentrated at the center O of the sphere.
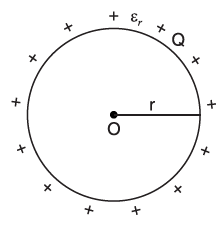
Potential at the surface of the sphere, V = Q / (4π * ɛr * ɛ0 * r)
Capacitance of sphere, the isolated sphere, C = Q / V = 4π * ɛr * ɛ0 * r
C = 4π * ɛr * ɛ0 * r… in a medium
= 4π * ε0 * r … in air
The following points may be noted :
The capacitance of sphere, an isolated spherical conductor is directly proportional to its radius. Therefore, for a given potential, a large spherical conductor (more r) will hold more charge Q (= CV) than the smaller one.
The Unit of ε0 = C/4πr = F/m.
Capacitance of Spherical Capacitor
We shall discuss two cases.
The capacitance of sphere, when the outer sphere is earthed
A spherical capacitor consists of two concentric hollow metallic spheres A and B which do not touch each other as shown. The outer sphere B is earthed while the electric charge is given to the inner sphere A. Let the medium of insulation be with relative permittivity εr between the spheres.
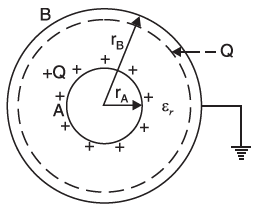
Let rA = radius of inner sphere A
rB = radius of outer sphere B
When a charge +Q is given to the inner sphere A, it induces a charge –Q on the inner surface of outer sphere B and +Q on the outer surface of B. Since sphere B is earthed, the +Q charge on its outer surface is neutralized by the earth.
Potential at inner sphere A, VA= [Q / (4π * ɛr * ɛ0 * rA)] + [-Q/ (4π * ɛr * ɛ0 * rB)]
= Q / (4π * ɛr * ɛ0) [1/rA – 1/rB]
=Q(rB – rA) / (4π * ɛr * ɛ0 * rA * rB)
Since the other sphere B is grounded, its potential is the same as ground potential zero (i.e., VB = 0).
Voltage between A and B, VAB = VA – VB = VA – 0 = VA
Capacitance of spherical capacitor, C = Q / VA = (4π * ɛr * ɛ0 * rA * rB) / (rB – rA)
C = Q / VA = (4π * ɛr * ɛ0 * rA * rB) / (rB – rA) in a medium,
C = Q / VA = (4π * ɛ0 * rA * rB) / (rB – rA) in air.
The capacitance of sphere, when the inner sphere is earthed
The system constitutes two capacitors in parallel. (a) The first capacitor (CBA) containing the inner surface of sphere B and the outer surface of sphere A. The capacitance of sphere is as found above
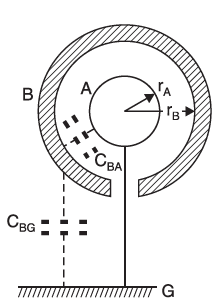
CBA= (4π * ɛr * ɛ0 * rA * rB) / (rB – rA)
The second capacitor (CBG) consists of the outer surface B and the ground G. Therefore, the capacitance matches the capacitance of an isolated sphere.
CBG = 4π ε0 rB … when the medium surrounding is air
Total capacitance = CBA + CBG
Unless it is mentioned, the outer sphere of a spherical capacitor is always assumed to be at ground potential which means it is earthed.
Factors affecting the capacitance of sphere
The factors influencing the capacitance are listed below:
Size of Spheres: It is evident from the formula that the capacitance is directly proportional to the radius of the spheres. The bigger the radii of the spheres the more will be capacitance as more charges will be attached to the enhanced surface area.
Size of dielectric: From the above formula for the capacitance of sphere, it is evident that the thickness of the dielectric (rB – rA) is inversely proportional to the capacitance. Hence, the increased size of the dielectric will hamper the capacitance making it inferior.
Selection of dielectric material: The relative permittivity of the dielectric ɛr is directly proportional to the sphere’s capacitance. Hence, the capacitance of sphere will be influenced by the selection of dielectric material.
Applications of Spherical capacitors
- Used in setups of precise capacitance measurement.
- Used for the protection of sensitive equipment in electrostatic shielding applications.
- Utilized for specialized sensing applications.

